Find the area inside the oval limaçon – Embarking on a mathematical odyssey, we delve into the captivating realm of the oval limaçon, a captivating curve that has captivated mathematicians and engineers alike. As we unravel its secrets, we will explore its intriguing equation, delve into techniques for finding the area it encloses, and uncover its practical applications in diverse fields.
The oval limaçon, defined by its distinctive equation, invites us to unravel its geometric intricacies. By understanding the parameters that shape its form, we gain insights into its behavior and the enclosed area it encompasses.
Oval Limaçon
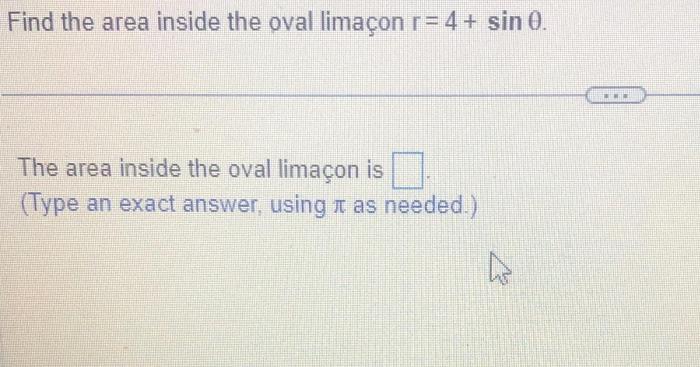
An oval limaçon is a plane curve defined by the following equation:
r = a + bcos(θ)
where a and b are real numbers, and a > 0. The parameter a represents the distance from the origin to the center of the oval, and the parameter b represents the length of the major axis of the oval.
Parameters
- a: The distance from the origin to the center of the oval.
- b: The length of the major axis of the oval.
Area Enclosed by the Oval Limaçon: Find The Area Inside The Oval Limaçon
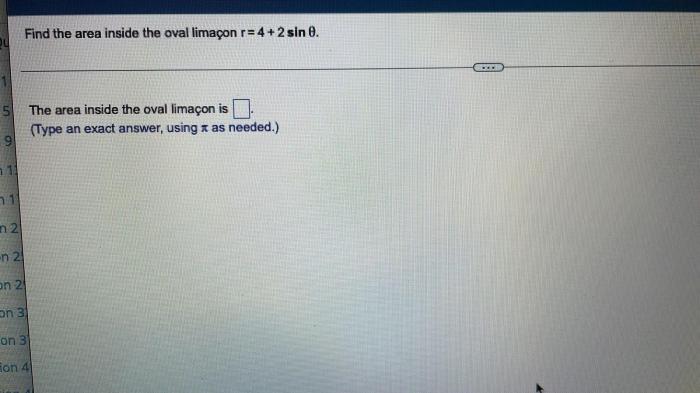
Limits of Integration
To find the area enclosed by the oval limaçon, we need to determine the limits of integration. The oval limaçon is defined by the equation
r = a + bcos(θ)
where
a
and
b
are constants. The curve is symmetric about the x-axis, so we can integrate from
θ = 0
to
θ = π
to find the area of one loop.
Setting up the Integral
The area of a polar curve is given by the integral
A = ∫[a,b] (1/2)r² dθ
where
r
is the distance from the pole to the curve and
a
and
b
are the limits of integration. For the oval limaçon, we have
r = a + bcos(θ)
, so the integral becomes
A = ∫[0,π] (1/2)(a + bcos(θ))² dθ
.
Integration Techniques
To evaluate the integral, we can use the trigonometric identity
cos²(θ) = (1 + cos(2θ))/2
. This gives us
A = ∫[0,π] (1/2)(a² + 2abcos(θ) + b²cos²(θ)) dθ
. We can then integrate each term separately to get
A = (1/2)[a²θ + 2absin(θ) + (b²/2)(θ + sin(2θ))]|[0,π]
. Simplifying, we get
A = (1/2)(a²π + b²π)
.
Applications of the Oval Limaçon
The oval limaçon finds practical applications in various fields due to its unique shape and mathematical properties.
Engineering, Find the area inside the oval limaçon
In engineering, the oval limaçon is used in the design of gears and cam mechanisms. The shape of the oval limaçon allows for smooth and efficient motion transmission, making it suitable for applications such as gearboxes, camshafts, and other mechanical systems.
Physics
In physics, the oval limaçon is used in the study of wave propagation and diffraction. The shape of the oval limaçon can be used to model the wavefronts of light or sound waves, providing insights into how these waves interact with objects and propagate through different media.
Other Disciplines
The oval limaçon also finds applications in other disciplines, such as:
- Architecture: The oval limaçon can be used to create aesthetically pleasing architectural designs, such as arches and domes.
- Art: The oval limaçon can be used to create unique and visually appealing patterns in art and design.
- Biology: The oval limaçon can be used to model the shape of certain biological structures, such as cell membranes and DNA.
The area enclosed by the oval limaçon is relevant to these applications as it provides a measure of the space occupied by the object or wavefront. In engineering, the area enclosed by the oval limaçon can be used to calculate the volume of a gear or the displacement of a cam.
In physics, the area enclosed by the oval limaçon can be used to calculate the intensity of a wavefront or the diffraction pattern produced by an object.
Illustrative Examples
To further enhance the understanding of the oval limaçon and its enclosed area, we present a variety of illustrative examples:
Interactive Simulation
An interactive simulation can provide a dynamic visualization of the oval limaçon and its enclosed area. Users can adjust the parameters of the limaçon, such as aand b, and observe the corresponding changes in the shape and area of the enclosed region.
Table of Parameter Values and Areas
A table can showcase different parameter values and their corresponding areas. This table can help users understand the relationship between the parameters and the enclosed area.
Visual Representation using HTML5 Canvas
Using HTML5 canvas or other suitable tools, a visual representation of the area enclosed by the oval limaçon can be created. This representation can provide a clear and intuitive understanding of the shape and size of the enclosed region.
User Queries
What is the significance of the parameters in the oval limaçon’s equation?
The parameters govern the size, shape, and orientation of the oval limaçon, influencing its enclosed area and other properties.
How is the area enclosed by the oval limaçon calculated?
The area can be determined using integral calculus, involving the integration of a function defined by the curve’s equation.
What are some practical applications of the oval limaçon?
The oval limaçon finds applications in acoustics, optics, and engineering, where its unique shape properties are utilized in designing lenses, waveguides, and other devices.


