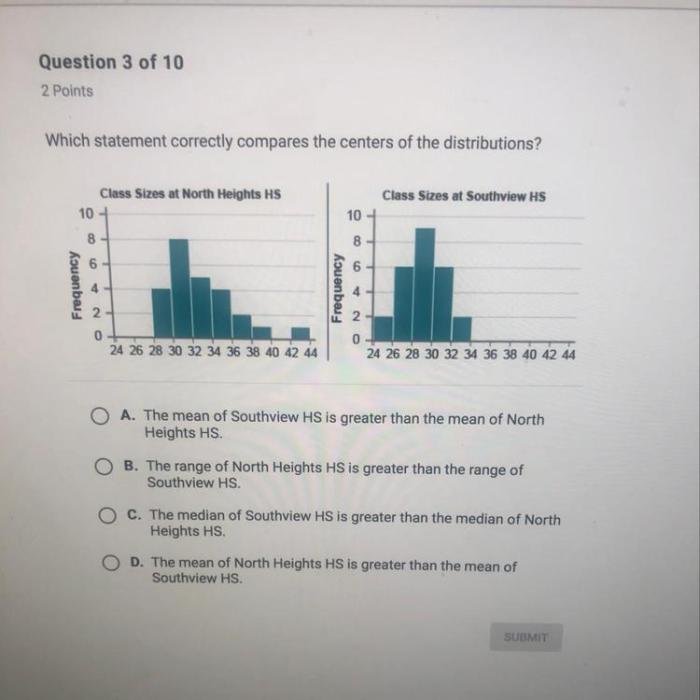
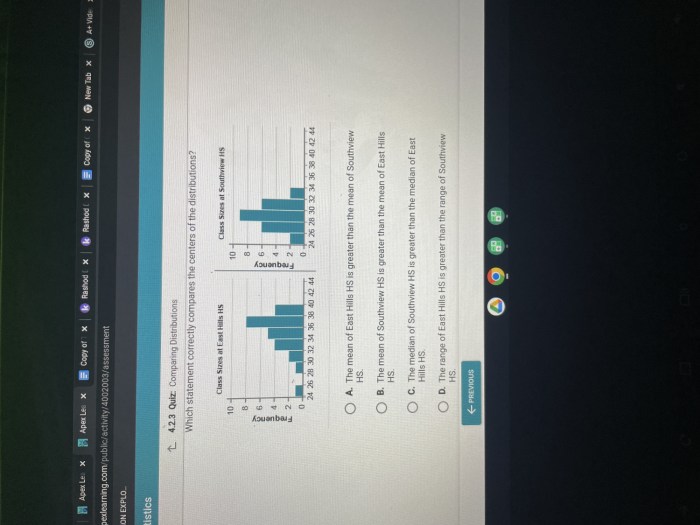
Which statement correctly compares the centers of the distributions – This exploration delves into the concept of central tendency and its various measures, providing a comprehensive understanding of how to compare the centers of distributions. By examining the strengths and weaknesses of different measures, we gain insights into making informed comparisons and visualizing the results effectively.
Delving deeper, we uncover the intricacies of comparing multiple distributions, addressing the challenges and considerations involved. Through illustrative examples, we demonstrate the practical application of these concepts, empowering readers with the knowledge to analyze and interpret data with precision.
Comparing Centers of Distributions

In statistics, the central tendency of a distribution refers to the middle or average value of the data. It provides a measure of the typical value in a dataset. There are three commonly used measures of central tendency: mean, median, and mode.
The mean, also known as the average, is calculated by adding up all the values in a dataset and dividing by the number of values. The median is the middle value when the data is arranged in ascending order. The mode is the value that occurs most frequently in a dataset.
Comparing Two Distributions
When comparing the centers of two distributions, it is important to consider the strengths and weaknesses of each measure of central tendency. The mean is sensitive to outliers, which are extreme values that can significantly affect the average. The median is not affected by outliers, making it a more robust measure of central tendency.
However, the mean can be more informative than the median when the data is normally distributed.
To compare the centers of two distributions, we can calculate the difference between the means or medians of the two distributions. We can also calculate the standard deviation, which measures the spread of the data, to assess the variability of the two distributions.
Comparing Multiple Distributions, Which statement correctly compares the centers of the distributions
Comparing the centers of multiple distributions can be more challenging than comparing two distributions. One approach is to use a statistical test, such as the analysis of variance (ANOVA), to determine whether there are significant differences between the means of the multiple distributions.
Another approach is to use a graphical representation, such as a box plot, to visualize the distributions and compare their centers. Box plots show the median, quartiles, and outliers of a distribution, allowing for easy comparison of the central tendencies and variability of multiple distributions.
Visualizing the Comparison
Visualizing the comparison of the centers of distributions can help to identify patterns and trends in the data. Box plots, histograms, and scatterplots are commonly used methods for visualizing the comparison of distributions.
Box plots provide a graphical representation of the median, quartiles, and outliers of a distribution. Histograms show the frequency of occurrence of different values in a distribution. Scatterplots show the relationship between two variables, allowing for the comparison of the centers of distributions in different groups.
FAQ Guide: Which Statement Correctly Compares The Centers Of The Distributions
What is the most appropriate measure of central tendency for comparing distributions with outliers?
The median is less affected by outliers and provides a more robust measure of central tendency for such distributions.
How do I visualize the comparison of multiple distributions?
Box plots and histograms are effective methods for visualizing the comparison of multiple distributions, allowing for easy identification of differences in central tendency and spread.