Find the particular antiderivative that satisfies the following conditions: embark on an intriguing journey into the realm of antiderivatives, uncovering the fundamental principles and practical applications that govern these mathematical entities. This exploration will equip you with a comprehensive understanding of antiderivatives, empowering you to tackle complex problems with precision and confidence.
In this discourse, we will delve into the intricacies of antiderivatives, unraveling the power rule, sum/difference rule, chain rule, and substitution rule. Armed with these techniques, we will master the art of finding antiderivatives, unlocking their potential in real-world scenarios.
1. Introduction

An antiderivative of a function is a function whose derivative is the original function. In other words, the antiderivative of f(x) is a function F(x) such that F'(x) = f(x). Antiderivatives are closely related to integration, which is the process of finding the area under a curve.
In this article, we will discuss how to find the particular antiderivative that satisfies certain given conditions.
2. Methods for Finding Antiderivatives: Find The Particular Antiderivative That Satisfies The Following Conditions:
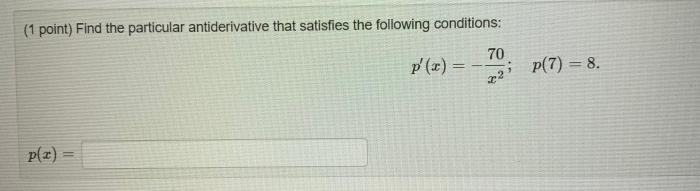
There are several methods for finding antiderivatives. The most common methods are the power rule, the sum/difference rule, the chain rule, and the substitution rule.
2.1. Power Rule
The power rule states that the antiderivative of x nis (1/(n+1))x n+1, where n is any real number except -1. For example, the antiderivative of x 3is (1/4)x 4.
2.2. Sum/Difference Rule
The sum/difference rule states that the antiderivative of f(x) + g(x) is F(x) + G(x), where F(x) is the antiderivative of f(x) and G(x) is the antiderivative of g(x). For example, the antiderivative of x 2+ 2x is (1/3)x 3+ x 2.
2.3. Chain Rule
The chain rule states that the antiderivative of f(g(x)) is F(g(x)) – g'(x), where F(x) is the antiderivative of f(x) and g'(x) is the derivative of g(x). For example, the antiderivative of sin(x 2) is -cos(x 2).
2.4. Substitution Rule
The substitution rule states that the antiderivative of f(u)du is F(u) + C, where F(u) is the antiderivative of f(u) and C is an arbitrary constant. For example, the antiderivative of 2x 2+ 1 is (2/3)x 3+ x + C.
3. Applying Methods to Satisfy Conditions

To find the particular antiderivative that satisfies certain given conditions, we need to use the appropriate method or combination of methods.
3.1. Power Rule
If the given function is a power function, we can use the power rule to find the antiderivative.
3.2. Sum/Difference Rule
If the given function is a sum or difference of functions, we can use the sum/difference rule to find the antiderivative.
3.3. Chain Rule
If the given function is a composite function, we can use the chain rule to find the antiderivative.
3.4. Substitution Rule, Find the particular antiderivative that satisfies the following conditions:
If the given function involves a substitution variable, we can use the substitution rule to find the antiderivative.
4. Examples and Applications
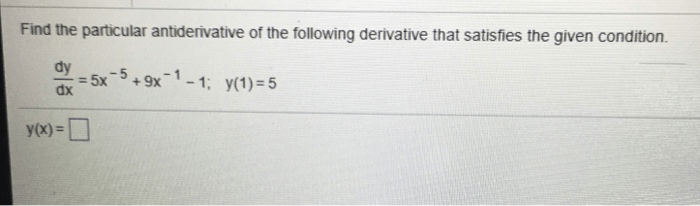
Here are some examples of how to find antiderivatives using different methods.
- Find the antiderivative of x 3+ 2x. Using the sum/difference rule, we get ∫(x 3+ 2x)dx = ∫x 3dx + ∫2xdx = (1/4)x 4+ x 2+ C.
- Find the antiderivative of sin(x 2). Using the chain rule, we get ∫sin(x 2)dx = -cos(x 2) + C.
- Find the antiderivative of 2x 2+ 1. Using the power rule and the sum/difference rule, we get ∫(2x 2+ 1)dx = (2/3)x 3+ x + C.
Antiderivatives have many applications in real-world scenarios. For example, they can be used to find the area under a curve or to calculate the volume of a solid of revolution.
Question & Answer Hub
What is an antiderivative?
An antiderivative of a function is a function whose derivative is the original function.
How do I find the antiderivative of a function?
There are several methods for finding antiderivatives, including the power rule, sum/difference rule, chain rule, and substitution rule.
What are the applications of antiderivatives?
Antiderivatives have numerous applications, including finding the area under a curve, calculating the volume of a solid of revolution, and solving differential equations.